ShiXiang
/
RobotKernal-UESTC
forked from logzhan/RobotKernal-UESTC
1
0
Fork 0
Code Pull Requests Activity
RobotKernal-UESTC/Docs/UWB解算原理.md

3.3 KiB
Raw Permalink Blame History

UWB 定位原理

1.三维坐标转二维坐标

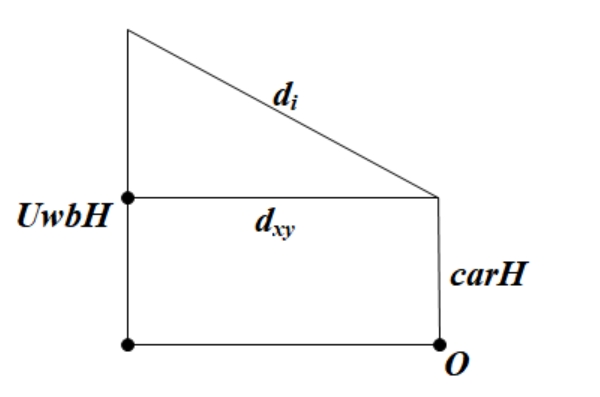
​ 在割草机器人项目中，割草机器人目前只考虑二维平面的定位。但是UWB测量的距离是三维距离，所以我们根据机器人的高度carH和UWB标签的高度UwbH计算出水平距离dxy。

// dxy^2 = di^2 - (UwbH = carH)^2 
for(int i=0; i<3; i++){
	this->d[i] = sqrt(this->d[i] * this->d[i] - (AnchorPos[i][2] - CARHEIGHT) * 
                     (AnchorPos[i][2] - CARHEIGHT));
}

UWB高度修正

2.多项式拟合

​ UWB的定位是存在波动的，所以会根据UWB计算距离的规律对计算的距离进行多项式拟合，可以起到滤波提高精度作用。下面的计算实际是收集不同实测距离下，UWB的实际输出距离，利用3次多项式拟合得到的结果。

​ 下面的计算跟标签的位置以及高度无关，主要跟UWB的硬件设备的特性有关。

d[0] = ((((4.9083e-07 * d[0]) - 4.6166e-04) * d[0]) + 1.0789) * d[0] + 5.4539;
d[1] = ((((-4.1679e-07 * d[1]) + 5.0999e-04) * d[1]) + 0.7930) * d[1] + 29.8296;
d[2] = ((((2.3514e-07 * d[2]) - 1.8277e-04) * d[2]) + 0.9935) * d[2] + 9.8852;

3.位置求解

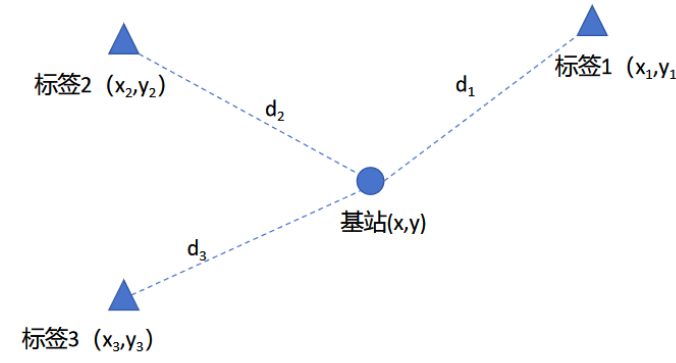
​ UWB位置求解采用如下图示：

UWB位置示意图

​ UWB的定位可以用下面公式描述, 其中(x,y)是割草机器人上面的UWB的位置，另外三个坐标点是3个UWB标签的位置，可以有如下的公式。


d_1^2 = (x_1 - x)^2 + (y_1 - y)^2   \space\space\space\space\space (1)\\
d_2^2 = (x_2 - x)^2 + (y_2 - y)^2   \space\space\space\space\space(2)\\
d_3^2 = (x_3 - x)^2 + (y_3 - y)^2   \space\space\space\space\space(3)\\

​ (2)-(1)以及(3)-(2)消去二次项，可得：


d_1^2 - d_2^2 = \left[ -2(x_1 - x_2)x + x_1^2 - x_2^2 \right] + \left[ -2(y_1 - y_2)y + y_1^2 - y_2^2 \right] \\

d_1^2 - d_3^2 = \left[ -2(x_1 - x_3)x + x_1^2 - x_3^2 \right] + \left[ -2(y_1 - y_3)y + y_1^2 - y_3^2 \right]

​ 整理为矩阵形式：


-2 \begin{bmatrix}
x_1 - x_2 & y_1 - y_2 \\
x_1 - x_3 & y_1 - y_3
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}
=
\begin{bmatrix}
(d_1^2 - d_2^2) - (x_1^2 - x_3^2) - (y_1^2 - y_3^2) \\
(d_1^2 - d_3^2) - (x_1^2 - x_3^2) - (y_1^2 - y_3^2)
\end{bmatrix}

​ 整理可得：


\begin{align*}
A &= -2\cdot \begin{bmatrix}
x_1 - x_2 & y_1 - y_2 \\
x_1 - x_3 & y_1 - y_3
\end{bmatrix}\\
b &= \begin{bmatrix}
(d_1^2 - d_2^2) - (x_1^2 - x_2^2) - (y_1^2 - y_2^2) \\
(d_1^2 - d_3^2) - (x_1^2 - x_3^2) - (y_1^2 - y_3^2)
\end{bmatrix}\\
X &= \begin{bmatrix}
x\\
y
\end{bmatrix}
\end{align*}

​ 矩阵A对应的代码：

for(int i=0; i<2; i++){
    A.mat[i][0] = -2*(this->AnchorPos[0][0]-this->AnchorPos[i+1][0]);
    A.mat[i][1] = -2*(this->AnchorPos[0][1]-this->AnchorPos[i+1][1]);
}

​ 矩阵b对应的代码：

for(int i=0; i<2; i++)
{
	b.mat[i][0] = (this->d[0]*this->d[0]-this->d[i+1]*this->d[i+1])\
     - (this->AnchorPos[0][0]*this->AnchorPos[0][0]-this->AnchorPos[i+1][0]*this->AnchorPos[i+1][0]) 
     - (this->AnchorPos[0][1]*this->AnchorPos[0][1]-this->AnchorPos[i+1][1]*this->AnchorPos[i+1][1]);
}

​ 那么，上述矩阵可以通过X=(A^T\cdot A)^{-1}A^T*b 求解UWB的位置。

Mat AT=~A;
uwbPos=(AT*A)%AT*b;
this->uwb_data_.x_ = uwbPos.mat[0][0];
this->uwb_data_.y_ = uwbPos.mat[1][0];